If you carry a penny in your coin tray, how long would it take for that penny to cost you more than a cent in extra gas?

—Leto Atreides

At current prices, 140,000 miles, close to the average car’s lifetime mileage:

\[1\text{ cent}\times\left ( \frac{30\frac{\text{miles}}{\text{gallon}}} {\frac{2.73\text{ grams}}{50\text{ pounds}}\times0.5%\times\frac{$3.50}{\text{gallon}}} \right )\approx140,000\text{ miles}\]

That means that as long as you go through pennies faster than you go through cars, you’re coming out ahead. (The equation assumes, for a 30 mpg car, 50 lbs of cargo means a 0.5% hit in fuel economy.)

But gas money isn’t the only cost attached to a penny. Let’s consider some of the others.

Suppose you found it on the ground on the way to your car. How much did it cost you to pick it up in the first place?

How much is your time worth? This obviously depends on a lot of things and varies from time to time and person to person. But for a broad estimate, I sometimes use a ballpark value of $10/hour—which is somewhere between the US minimum wage and the average wage—but you can adjust up or down to fit your preference.

If your time is worth $10 an hour, a penny is worth 3.6 seconds. If spotting and picking up a penny takes you more than 3.6 seconds, it’s a loss.

Of course, picking it up isn’t the only time cost. Having a penny in your pocket makes it harder to find other things there, so you might spend more time looking for stuff in the future.

And then there’s the future time spent dealing with the penny. You may spend time figuring out if it helps you make change, putting it in a roll, donating them, or doing countless other hard-to-predict things. (You may argue that dropping them in a donation jar is noble enough that it makes picking them up worthwhile. That may be true; it’s what I do with pennies. But this isn’t an argument against donating money—it’s just an argument that picking up pennies may not be an efficient way to use your time to acquire money to donate.)

There’s another cost (and benefit) to picking up a penny—the calories burned. When you crouch to pick up a penny, you expend energy. A 70-kilogram person who lowers their center of mass by half a meter will burn about half a calorie of energy standing back up:

\[\frac{70\text{ kg}\times\text{Earth Gravity}\times50\text{ centimeters}}{20\%}=1.72\text{ kJ}=0.41\text{ food calories}\]

(The “20%” represents the overall energy efficiency of the squatting process, which I based on the efficiency of stair climbing.)

All else being equal, to replenish those 0.41 extra calories, you’ll need to eat 0.41 calories worth of extra food. And food costs money.

Donuts provide 836 calories per dollar, or 8.3 calories per penny—plenty to supply the 0.41 needed to pick one up. On the other hand, if you get your energy from expensive fresh strawberries, you might only get 20 calories per dollar—meaning that picking up that penny costs you 2 cents in extra strawberry. (In dollars per calorie, the cheapest energy sources in the supermarket are refined sugar, oil, and shortening).

But on the other hand, burning calories is exercise, which is good for you. Crouching to pick up that penny is equivalent to two or three seconds on an exercise machine. What’s that worth?

Well, one study suggests that 15 minutes of moderate exercise per day adds three years to your life expectancy (with smaller improvements in mortality rate for progressively more daily exercise). It’s a tremendous oversimplification, but a crude back-of-the-envelope estimate suggests each calorie burned adds something like 30 seconds to your life—or 12 seconds per penny.

But wait—if it only takes a couple seconds to pick up a penny, but it pays back 12 seconds, then you could game the system by repeatedly dropping a penny and picking it back up ...

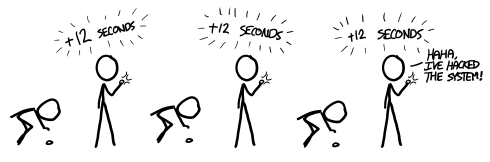
… which is just another way of saying that exercise is a good idea.

One final thought:

This article is about 770 words long. If you read at 250 words per minute, then add in another couple minutes for the drawings and equations, then reading this article has eaten up 300 seconds of your time. At $10/hour, that’s 83 cents.

Which means that by reading this article, you’ve quite possibly erased the gains from all the pennies you’ll pick up in your entire life and any gains in fuel economy due to keeping a clean change cup.

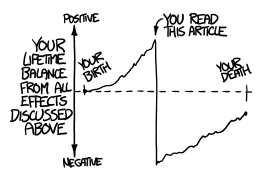
You’re welcome.