Could I cool down the Earth by capturing a comet and dropping it in the ocean, like an ice cube in a glass of water?
Daniel Becker
No. In fact, it's honestly sort of impressive to find a solution that would actively make the problem worse in so many different ways.

Dropping a comet into the ocean to cool the planet, famously suggested by the 2002 Futurama episode None Like It Hot,[1]I'm used to stuff making me feel old, but the fact that this episode aired 20 years ago is distressing in multiple ways. wouldn't work for a few reasons.
One is that dropping things from space creates heat. When water—or anything else—falls, it gains kinetic energy. When it stops falling, that energy has to go somewhere. Generally, it turns into heat. Water that goes over Niagara Falls, for example, gains enough kinetic energy during the 50-meter plunge to warm it up by about 0.1°C by the time it reaches the bottom. (This added heat is minor compared to the cooling effects of evaporation on the way down, so the actual temperature at the bottom is likely colder.)
Outer space is a lot higher up than Niagara Falls,[citation needed] so the plunge down into the atmosphere at the bottom of Earth's gravity well adds a lot more than 0.1 degrees worth of heat. A chunk of ice from space that falls to Earth gains enough energy to warm the ice up, melt it, boil it into vapor, and then heat the vapor to thousands of degrees. If you built an icy waterfall from space, the water would arrive at the bottom as a river of superheated steam.

Small chunks of ice falling from space disintegrate and boil away before they reach the ground, warming the upper atmosphere. Large comets can reach the ground intact and be vaporized on impact as their kinetic energy is converted to heat all at once. This heat energy would be about 100 times greater than the energy needed to bring even a very cold comet up to room temperature, so a comet falling from space would heat the Earth 100 times more than it cooled it.

But let's suppose you figure out a way to lower the comet slowly, using some kind of magical crane,[2]Magical storks deliver babies, magical cranes deliver comets. and gently set the comet in the ocean.

Comets are more dust than ice, but they're not particularly dense. A tiny piece of a comet would float for a short time until it became waterlogged, melted, and broke apart. A full-size comet wouldn't be strong enough to support its own weight, and would collapse like a drying sand sculpture.
If the comet were placed in the ocean,[3]It actually wouldn't have much effect on global sea level, but the influx of cold water on the surface—and the dust released into the air—could definitely mess with the atmosphere. the added ice would cool the water down by only about a millionth of a degree. If you set the comet on land, it would soak up heat from the atmosphere—which contains much less stored heat than the oceans—briefly cooling the air by an average of one or two thousandths of a degree.
Okay, so we just need thousands of comets, right? Each one will cool the air a little bit. With a large enough supply of comets, we can keep the Earth nice and cool, as long as we make sure they're lowered slowly.
Unfortunately, comets would affect the Earth's temperature in another way. In addition to dust and water, they contain a small amount of CO2, which would be released into the atmosphere as the comet melted. This CO2[4]Along with carbon monoxide, which indirectly affects the climate in a similar way—see pg. 718-719 of the IPCC WG1 AR5 report for more. would change Earth's radiation balance, trapping heat near the surface and raising the planet's temperature. After a few years, the comet's greenhouse effect would have trapped more heat than the ice absorbed, and over the decades to follow, the extra heat would keep piling up.
The CO2 released from the comet would raise the temperature of the Earth for centuries. It wouldn't just cancel out the cooling effect of the ice—over time, the comet's greenhouse effect would deliver as much heat as if you'd just let it slam into the planet and vaporize.[5]Although letting a comet slowly decay on the surface would definitely be preferable to a high-speed impact, as any dinosaur from the end of the Cretaceous can tell you.
It's okay. Despite all this, your scenario could fix global warming.
Remember that hypothetical crane that lets you lower comets to the surface? Well, if you hooked it up to a generator, you could use the slowly-descending comet to produce electricity.
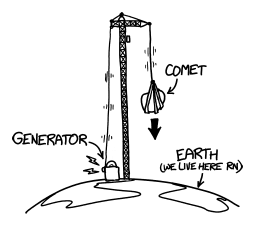
One comet, lowered from space down to the surface, could supply the entire world's energy consumption for a year. Sure, it would release a little CO2, but it would be nothing compared to the pollution from our current sources of energy. A comet crane generator could cut our energy-related greenhouse gas emissions to almost zero. The comet isn't the important part, the crane is.
Sadly, we don't have the technology to build comet-lowering cranes—certainly not in time to help mitigate climate change. But harvesting orbital energy like this is a neat idea! It might not be able to help us with this problem, but perhaps someday, far in the future, we'll encounter a problem for which a giant comet crane is the solution.