If you stripped away all the rules of car racing and had a contest which was simply to get a human being around a track 200 times as fast as possible, what strategy would win? Let's say the racer has to survive.
Hunter Freyer
The best you'll be able to do is about 90 minutes.
There are lots of ways you could build your vehicle—an electric car,[1]With wheels designed to dig into the pavement on turns. a rocket sled, or a carriage that runs along a rail on the track—but in each case, it's pretty easy to develop the design to the point where the human is the weakest part.
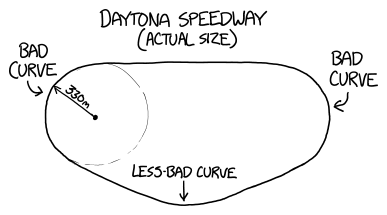
The problem is acceleration. On the curved parts of the track, drivers will feel powerful G forces.[2]Which you can broadly call either "centrifugal" or "centripetal" forces, depending on exactly which type of pedant you want to annoy. The Daytona Speedway in Florida has two main curves, and if the vehicles go around them too fast, the drivers will die from the acceleration alone.
For extremely brief periods, such as during car accidents, people can experience hundreds of Gs and survive. (One G is the pull you feel when standing on the ground under Earth's gravity.) Fighter pilots can experience up to 10 Gs during maneuvers, and—perhaps because of that—10 Gs is often used as a rough limit for what people can handle. However, fighter pilots only experience 10 Gs very briefly. Our driver would be experiencing them, in pulses, for minutes and probably hours.
There's a good NASA document on the physical effects of acceleration here, and a particularly helpful chart in Figure 5 here.
But the most fun data comes from John Paul Stapp. Stapp was an Air Force officer who strapped himself into a rocket sled and pushed his body to the limit, taking careful notes after every run. You can read a great essay about him on the Ejection Site. The whole story is fascinating, but my favorite line is, "... Stapp was promoted to the rank of major [and] reminded of the 18 G limit of human survivability ..."
Stapp aside, the data shows that for periods on the order of an hour, normal humans can only handle 3-6 Gs of acceleration. If we limit our vehicle to 4 Gs, its top speed on the turns at Daytona will be about 240 mph. At this speed, the course will take about 2 hours to complete—which is definitely faster than anyone has driven it in an actual car, but not by that much.
But wait! What about the straightaways? The vehicle will be accelerating during the turns, but coasting on the straightaways. We could instead accelerate the vehicle up to a higher speed while on straight segments, then decelerate it back down when approaching the end. This would result in a speed profile like this:

This has the additional advantage that—with some clever back-and-forth maneuvering on the track—the driver can be kept at a relatively constant acceleration through the whole trip, hopefully making the forces easier to endure.

Keep in mind that the direction of the acceleration will keep changing. Humans can survive acceleration best if they're accelerated forward, in the direction of their chest, like a driver accelerating forward. The body is least capable of being accelerated downward toward the feet, which causes blood to pile up in the head. To keep our driver alive, we'll need to swivel them around so they're always being pressed against their back. (But we have to be careful not to change direction too fast, or the centrifᵫtal[3]Splitting the difference. force from the swiveling of the seat will itself become deadly!)
The fastest modern Daytona racers take about 3 hours to finish the 200 laps. If limited to 4 Gs, our driver will finish the course in a little under an hour and 45 minutes. If we raise the limit to 6 Gs, the time drops to an hour and 20. At 10 Gs—well past human tolerability—it would still take an hour. (It would also involve breaking the sound barrier on the backstretch.)
So, barring dubious concepts like liquid breathing, human biology limits us to Daytona finishing times over an hour. What if we drop the "survive" requirement? How fast can we get the vehicle to go around the track?
Imagine a "vehicle" anchored with Kevlar straps to a pivot in the center, reinforced with a counterweight on the other side. In effect, this is a giant centrifuge. This lets us apply one of my favorite weird equations,[4]See footnote [8] in article #86. which says that the edge of a spinning disc can't go faster than the square root of the specific strength[5](tensile strength divided by density) of the material it's made of. For strong materials like Kevlar, this speed is 1-2 km/s. At those speeds, a capsule could conceivably finish the race in about 10 minutes—although definitely not with a living driver inside.
Ok, forget the centrifuge. What if we build a solid chute, like a bobsled course, and send a ball bearing (our "vehicle") rocketing down it? Sadly, the disc equation strikes again—the ball bearing can't roll faster than a couple km/s or it will be spinning too fast and will tear itself apart.
Instead of making it roll, what if we make it slide? We could imagine a diamond cube sliding along a smooth diamond chute. Since it doesn't need to rotate, it could potentially survive more accelerations than a rolling ball bearing. However, the sliding would result in substantially more friction than the ball bearing example, and our diamond might catch fire.

To defeat friction, we could levitate the capsule with magnetic fields, and make it progressively smaller and lighter to accelerate and steer it more easily. Oops—we've accidentally built a particle accelerator.
And while it doesn't exactly fit the criteria in Hunter's question, a particle accelerator makes for a neat comparison. The particles in the LHC's beam go very close to the speed of light. At that speed, they complete 500 miles (30 laps) in 2.7 milliseconds.
Wikipedia lists about 850 motor racing tracks. The LHC beam could run the equivalent of a full Daytona 500 on each of those 850 tracks, one after another, in about 2 seconds, before the drivers had made it to the first turn.

And that's really as fast as you can go.