Tie Vote

What if there's LITERALLY a tie?

—Nate Silver (Twitter, January 4th, 2012)

In most states, a popular vote tie is broken by a coin toss or drawing names from a hat. The odds of a many-state tie are slimmer than the odds of the hat being hit by a bale of cocaine dumped from a drug-smuggling airplane.

Nate Silver flippantly posted his 'tie' question on Twitter during the tallying of the extremely close 2012 Republican Iowa Caucus results. In that case, an exact tie was averted—Santorum ended up winning by 34 votes out of 121,503. And since it was a non-binding nominating vote, the Iowa Republican Party could handle a tie any way they wanted.

But since it’s Election Day, let’s apply his question to the current contest. What will happen if there's a tie?

I don't mean an electoral college tie. There’s probably about a 1 in 500 chance of one of those this year, and the consequences are thoroughly explored. Instead, the question concerns both candidates getting the same number of votes in a state.

Several researchers—including Silver himself—have calculated the odds of a state winner being decided by a single vote, which is effectively the same as the probability of a tie vote. For typical close states, the linked article calculates the probabilities to be in the neighborhood of 1 in 100,000—which makes intuitive sense, since 100,000 is the sort of vote margin by which swing state elections are typically decided.

So what if there's a tie in a close state this year?

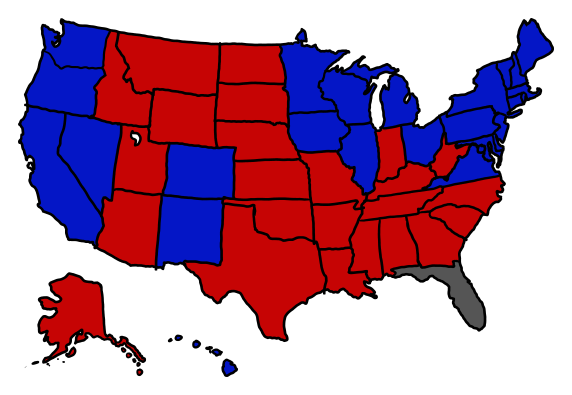
a map showing florida tied and all other states going as nate silver currently projects

For that matter, what if there’s a tie in every battleground state?

a map showing all battleground states tied

Well, for starters, recounts happen. But since recounts happen in close elections in general, these are just as likely to create ties as to break them. They don’t change the underlying probability. So let’s assume that after all recounts, there’s a tie. What then?

The short answer is that it’s up to the state’s laws.

I went through the general laws of nine competitive states to see how they handle popular vote ties. In most of them, the tie is broken by “drawing lots”—that is, randomly. (If you’re curious, here are links to some tie vote laws in each state: Virginia, North Carolina, Florida, Ohio, New Hampshire, Wisconsin, Colorado, Iowa, Nevada).

“Drawing lots” can mean a coin toss, drawing straws, or picking a name from a hat. Most states leave the details up to the Secretary of State or an electoral board, although Iowa Code 50.44 specifies that the names be written on pieces of paper and placed in a “receptacle”. In North Carolina, however, a tie vote (when more than 5,000 votes are cast) results in a new election. (Which could potentially itself result in a tie ...)

But let’s imagine that there’s not just one state that’s tied—instead, the nine most competitive states are tied (and the rest go as expected). If North Carolina held a runoff to break the tie, and the other eight states flipped coins (or picked from Iowa’s receptacle), Obama would be reelected in 431 out of 512 cases—about 84% of the time.

But how likely is a nine-state tie?

If we ballpark the odds of a tie vote in each close state at 1 in 100,000, then the odds of a tie vote in all nine states is in the neighborhood of one in a quattuordecillion—1 followed by 45 zeroes. (This ignores vote correlation between states, but it’s good enough for a first-order estimate).

Florida is hit by an average of 66 tornadoes per year. If each tornado is 50 yards wide and has a path 1.5 miles long (which is typical, if not necessarily the mean), we can calculate that a typical location in Florida experiences an average 1.4 picotornados per second:

\[66\tfrac{\text{tornadoes}}{\text{year}}\times\frac{1.5\text{ miles}\times50\text{ yards}}{\text{Area of Florida}}\approx1.4\times10^{-12}\tfrac{\text{tornadoes}}{\text{second}}\]

Astronomer Alan Harris calculates that a person’s lifetime odds of death from a comet or meteorite impact are about 1 in 700,000. If a typical person in the calculation lives 70 years, this suggests a Florida resident suffers an average of 0.64 femtodeaths per second from meteorite impacts:

\[\frac{\tfrac{1}{700,000}\text{deaths}}{70\text{ years}}\approx6.4\times10^{-16}\tfrac{\text{deaths}}{\text{second}}\]

In 1994, drug smugglers fleeing the authorities dropped an estimated 20 bales of cocaine from an airplane over Florida—one of which crashed through the roof of a Crime Watch meeting and narrowly missed the Homestead Chief of Police. If Florida has been hit by 20 bales of cocaine over the last 20 years, then the average person in Florida is struck by an average of 29 zeptobales of cocaine per second:

\[\frac{20\text{ bales}}{20\text{ years}}\times\frac{\left (\tfrac{75\text{ kg}}{\text{Density of cocaine}} \right )^\tfrac{2}{3}}{\text{Area of Florida}}\approx2.9\times10^{-21}\tfrac{\text{bales}}{\text{second}}\]

(By the way—this means that given a street price of $20,000 per kilogram, a typical acre of Florida land produces an average revenue of three cents per year in falling cocaine bales).

Putting all this together: The probability that every battleground state is exactly tied is roughly equal to the probability that, when one of the Florida electors reaches into the hat to draw a name, he or she is struck by a falling cocaine bale, the hat is hurled away within the next few seconds by a tornado, and the elector is obliterated minutes later by a meteorite impact.